..::Visualization with prosections   A prosection is a projection of a section. Visualizing 4D approximation sets using prosections works like this: Choose the 2D projection plane (for the sake of simplicity, let us assume this is f1f2), angle φ and distance d. These parameters define the section (the gray area in the left figure below). All vectors within this section are first orthogonally projected to the line crossing the origin and intersecting the f1-axis at angle φ, and finally rotated. For these transformations one of the following functions is used: 3D case: (f1, f2, f3) → (f1 cos φ + f2 sin φ, f3) 4D case: (f1, f2, f3, f4) → (f1 cos φ + f2 sin φ, f3, f4) The prosections are denoted as 3D(f1f2, φ, d) and 4D(f1f2, φ, d), respectively. All vectors outside the section are ignored. 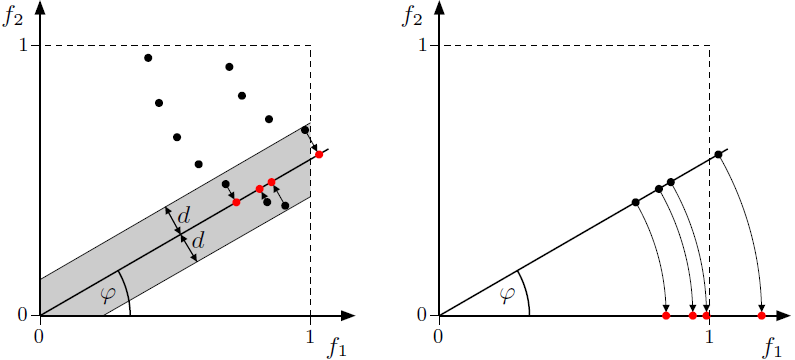Prosection Rotation Example: visualization of a discontinuous front   For this example we use an approximation set of discontinuous shape (as in the DTLZ test suite, thanks to the Walking Fish Group for making these approximation sets available online). The prosection matrix for the 3D case: 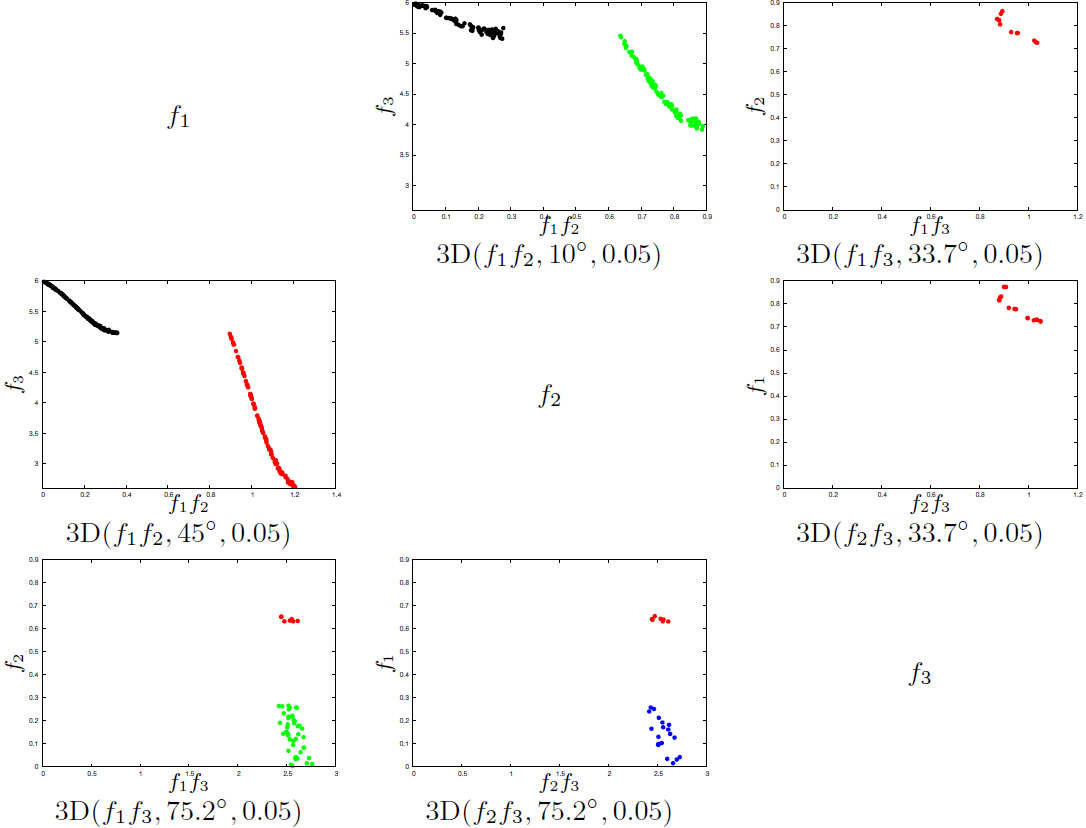The prosection matrix for the 4D case: 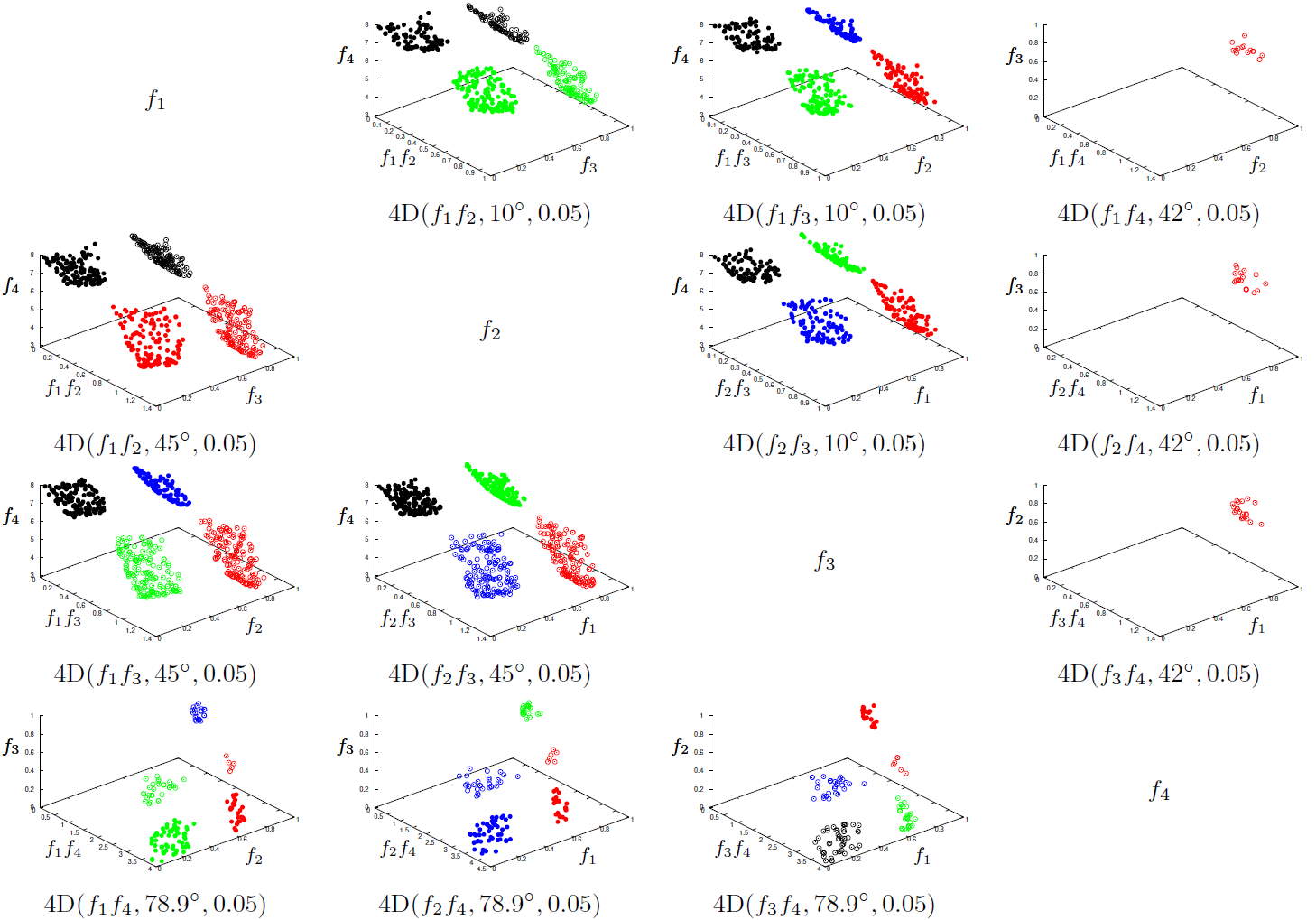Using gnuplot we can make an animation of the prosection matrix with angles going from 0 to 90°: 3D case: data files and gnuplot scripts (view readme) 4D case: data files and gnuplot scripts (view readme)