Surrogate Based Multiobjective Algorithm for Solving Computationally Expensive Numerical Problems Based on Relations Under Uncertainty
M. Mlakar (Supervised by B. Filipič)
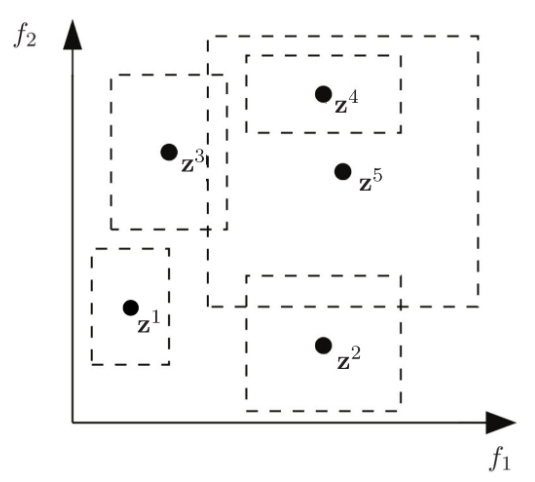
The goal of this doctoral research is to develop effective and efficient multiobjective optimization algorithm for solving hard numerical problems, where solution evaluation is computationally expensive. To achieve this goal the algorithm builds a surrogate model of the original objective function. With this surrogate model some solutions are then approximated and are used in the optimization process.
Project accomplished with a successful Ph.D. dissertation defense in April 2015.
